[R package] Calculate the responsiveness of each treatment relative to a control (Feat. deltactrl)

■ Quantifying Phenotypic Plasticity of Crops
In my previous posts, I explained how to quantify phenotypic plasticity of crops in response to environmental factors, and introduced the concept of responsiveness, calculated using the formula: (Treatment - Control) / Control, as shown in the table below.
| Genotype | Control | Treatment | Responsiveness |
| A | 100 | 90 | -10.0% = (90-100)/100 |
| B | 120 | 70 | -41.7% |
| C | 115 | 90 | -21.7% |
| D | 95 | 85 | -10.5% |
| E | 110 | 105 | -4.5% |
While calculating responsiveness for a single variable is relatively straightforward, it becomes more complex when grouping is involved—for example, calculating nitrogen responsiveness across different genotypes under various fungicide treatments. Performing such analyses by manually sorting and calculating in Excel can be time-consuming and error-prone.
To address this, I recently developed an R package called deltactrl. This package enables users to calculate responsiveness efficiently and consistently across multiple variables and grouping structures.
Here is one dataset.
if(!require(readr)) install.packages("readr")
library(readr)
github="https://raw.githubusercontent.com/agronomy4future/raw_data_practice/main/fertilizer_treatment.csv"
df= data.frame(read_csv(url(github),show_col_types = FALSE))
head(df,5)
Genotype Block variable value
1 Genotype_A I Control 42.9
2 Genotype_A II Control 41.6
3 Genotype_A III Control 28.9
4 Genotype_A IV Control 30.8
5 Genotype_B I Control 53.3
.
.
.
tail(df,5)
Genotype Block variable value
60 Genotype_C IV Fertilizer3 51.8
61 Genotype_D I Fertilizer3 71.6
62 Genotype_D II Fertilizer3 69.4
63 Genotype_D III Fertilizer3 56.6
64 Genotype_D IV Fertilizer3 47.4This data has two treatments (Genotype and Fertilizer) with 4 replicates.
xtabs(~variable + Genotype, data=df)
Genotype
variable Genotype_A Genotype_B Genotype_C Genotype_D
Control 4 4 4 4
Fertilizer1 4 4 4 4
Fertilizer2 4 4 4 4
Fertilizer3 4 4 4 4This graph represents the dataset.
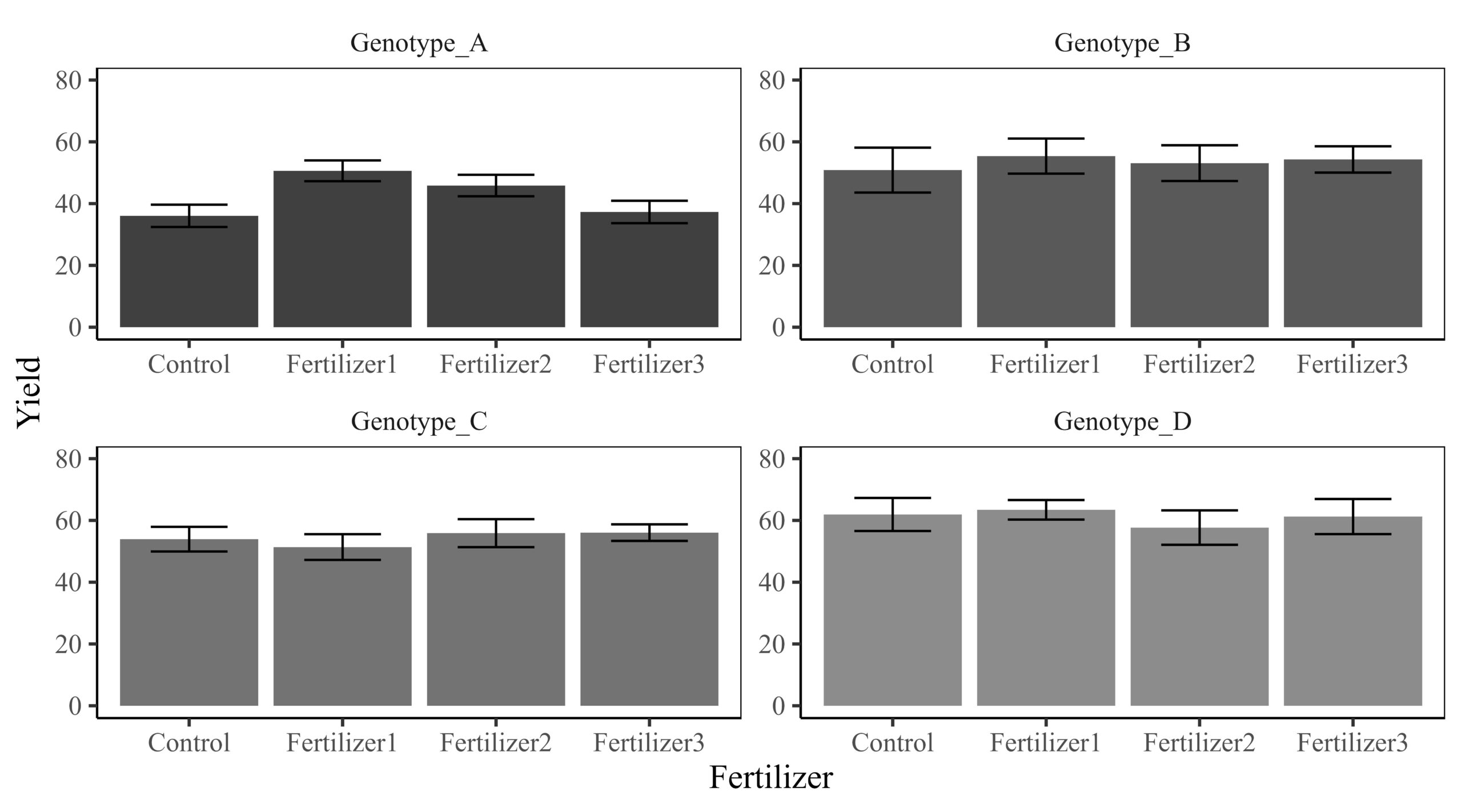
If we calculate responsiveness, we can omit the Control from the graph. The responsiveness metric will indicate how yields at different fertilizer levels deviate from the Control.

■ deltactrl package
First, let’s load the necessary library.
if(!require(remotes)) install.packages("remotes")
if (!requireNamespace("deltactrl", quietly = TRUE)) {
remotes::install_github("agronomy4future/deltactrl", force= TRUE)
}
library(remotes)
library(deltactrl)After loading the library, you can type ?deltactrl to view the details about the function.
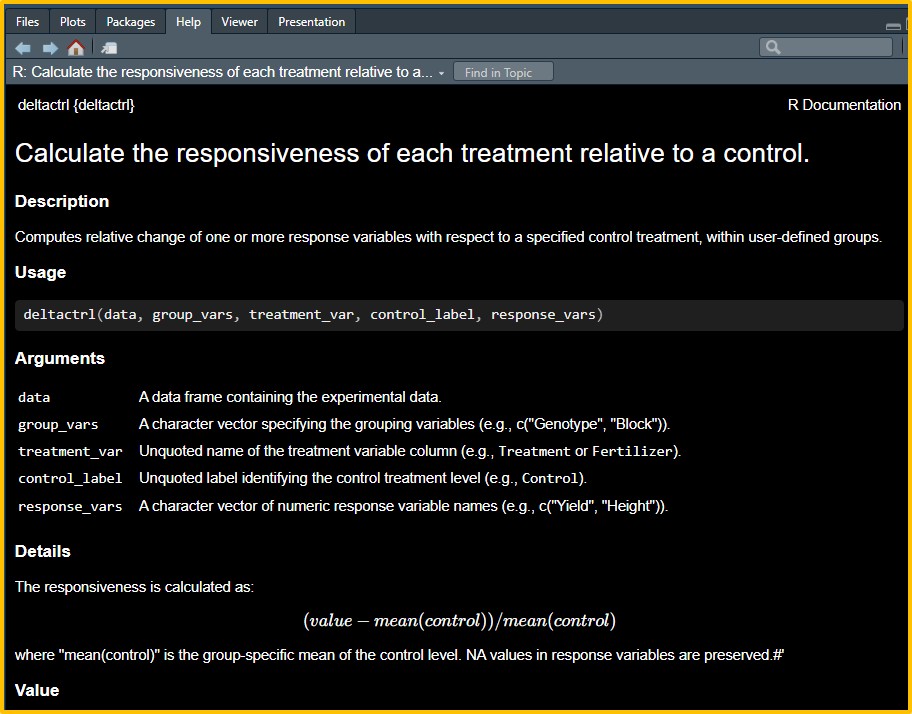
I will calculate responsiveness by grouping the data by genotype, using the ‘Control’ level in the ‘variable’ column as the baseline. The basic code structure will be as follows:
df2= deltactrl(
data= df,
group_vars= c("Genotype"),
treatment_var= variable,
control_label= Control,
response_vars= c("value")
)
print(df2, n = Inf)
Genotype Block variable value responsive_value
1 Genotype_A I Control 42.9 NA
2 Genotype_A II Control 41.6 NA
3 Genotype_A III Control 28.9 NA
4 Genotype_A IV Control 30.8 NA
5 Genotype_B I Control 53.3 NA
6 Genotype_B II Control 69.6 NA
7 Genotype_B III Control 45.4 NA
8 Genotype_B IV Control 35.1 NA
9 Genotype_C I Control 62.3 NA
10 Genotype_C II Control 58.5 NA
11 Genotype_C III Control 44.6 NA
12 Genotype_C IV Control 50.3 NA
13 Genotype_D I Control 75.4 NA
14 Genotype_D II Control 65.6 NA
15 Genotype_D III Control 54 NA
16 Genotype_D IV Control 52.7 NA
17 Genotype_A I Fertilizer1 53.8 0.492
18 Genotype_A II Fertilizer1 58.5 0.623
19 Genotype_A III Fertilizer1 43.9 0.218
20 Genotype_A IV Fertilizer1 46.3 0.284
21 Genotype_B I Fertilizer1 57.6 0.133
22 Genotype_B II Fertilizer1 69.6 0.369
23 Genotype_B III Fertilizer1 42.4 -0.166
24 Genotype_B IV Fertilizer1 51.9 0.0206
25 Genotype_C I Fertilizer1 63.4 0.176
26 Genotype_C II Fertilizer1 50.4 -0.0654
27 Genotype_C III Fertilizer1 45 -0.166
28 Genotype_C IV Fertilizer1 46.7 -0.134
29 Genotype_D I Fertilizer1 70.3 0.135
30 Genotype_D II Fertilizer1 67.3 0.0868
31 Genotype_D III Fertilizer1 57.6 -0.0698
32 Genotype_D IV Fertilizer1 58.5 -0.0553
33 Genotype_A I Fertilizer2 49.5 0.373
34 Genotype_A II Fertilizer2 53.8 0.492
35 Genotype_A III Fertilizer2 40.7 0.129
36 Genotype_A IV Fertilizer2 39.4 0.0929
37 Genotype_B I Fertilizer2 59.8 0.176
38 Genotype_B II Fertilizer2 65.8 0.294
39 Genotype_B III Fertilizer2 41.4 -0.186
40 Genotype_B IV Fertilizer2 45.4 -0.107
41 Genotype_C I Fertilizer2 64.5 0.196
42 Genotype_C II Fertilizer2 46.1 -0.145
43 Genotype_C III Fertilizer2 62.6 0.161
44 Genotype_C IV Fertilizer2 50.3 -0.0672
45 Genotype_D I Fertilizer2 68.8 0.111
46 Genotype_D II Fertilizer2 65.3 0.0545
47 Genotype_D III Fertilizer2 45.6 -0.264
48 Genotype_D IV Fertilizer2 51 -0.176
49 Genotype_A I Fertilizer3 44.4 0.232
50 Genotype_A II Fertilizer3 41.8 0.160
51 Genotype_A III Fertilizer3 28.3 -0.215
52 Genotype_A IV Fertilizer3 34.7 -0.0374
53 Genotype_B I Fertilizer3 64.1 0.261
54 Genotype_B II Fertilizer3 57.4 0.129
55 Genotype_B III Fertilizer3 44.1 -0.133
56 Genotype_B IV Fertilizer3 51.6 0.0147
57 Genotype_C I Fertilizer3 63.6 0.179
58 Genotype_C II Fertilizer3 56.1 0.0403
59 Genotype_C III Fertilizer3 52.7 -0.0227
60 Genotype_C IV Fertilizer3 51.8 -0.0394
61 Genotype_D I Fertilizer3 71.6 0.156
62 Genotype_D II Fertilizer3 69.4 0.121
63 Genotype_D III Fertilizer3 56.6 -0.0860
64 Genotype_D IV Fertilizer3 47.4 -0.235 The responsiveness relative to the Control was calculated for each genotype. Now, let’s create a figure to visualize the results. First, the data needs to be summarized to generate a bar graph.
df3= data.frame(subset (df2, variable!="Control") %>%
group_by(Genotype, variable) %>%
dplyr::summarize(across(c(responsive_value),
.fns= list(Mean=~mean(., na.rm= TRUE),
SD= ~sd(., na.rm= TRUE),
n=~length(.),
se=~sd(.,na.rm= TRUE) / sqrt(length(.))))))
print(df3)
Genotype variable responsive_value_Mean responsive_value_SD responsive_value_n responsive_value_se
1 Genotype_A Fertilizer1 0.40429958 0.18678735 4 0.09339368
2 Genotype_A Fertilizer2 0.27184466 0.19261643 4 0.09630821
3 Genotype_A Fertilizer3 0.03467406 0.20157613 4 0.10078807
4 Genotype_B Fertilizer1 0.08898722 0.22356907 4 0.11178453
5 Genotype_B Fertilizer2 0.04424779 0.22774865 4 0.11387433
6 Genotype_B Fertilizer3 0.06784661 0.16724697 4 0.08362349
7 Genotype_C Fertilizer1 -0.04728790 0.15442957 4 0.07721479
8 Genotype_C Fertilizer2 0.03616134 0.16801000 4 0.08400500
9 Genotype_C Fertilizer3 0.03940658 0.09945565 4 0.04972782
10 Genotype_D Fertilizer1 0.02422285 0.10233126 4 0.05116563
11 Genotype_D Fertilizer2 -0.06863141 0.17988747 4 0.08994374
12 Genotype_D Fertilizer3 -0.01090028 0.18341009 4 0.09170505Second, I will generate the figure.
if(!require(ggplot2)) install.packages("ggplot2")
library(ggplot2)
Fig2=ggplot(data=df3, aes(x=variable, y=responsive_value_Mean, fill=Genotype)) +
geom_bar(stat="identity",position="dodge", width=0.9, size=1) +
geom_errorbar(aes(ymin=responsive_value_Mean-responsive_value_se, ymax=responsive_value_Mean+responsive_value_se),
position=position_dodge(0.5), width=0.5) +
scale_fill_manual(values=c("grey25","grey35","grey45","grey55"))+
scale_y_continuous(breaks = seq(-0.6, 0.6, 0.3), limits = c(-0.6, 0.6)) +
geom_hline(yintercept=0, linetype="dashed", color="red", size=1) +
facet_wrap(~ Genotype, scales="free") +
labs(x="Fertilizer", y="Yield") +
theme_classic(base_size= 15, base_family = "serif") +
theme(legend.position="none",
legend.title=element_blank(),
legend.key=element_rect(color="white", fill=alpha(0.5)),
legend.text=element_text(family="serif", face="plain",
size=13, color="black"),
legend.background= element_rect(fill=alpha(0.5)),
panel.border= element_rect(color="black", fill=NA, linewidth=0.5),
axis.line= element_line(linewidth= 0.5, colour= "black"),
strip.background=element_rect(color="white",
linewidth=0.5, linetype="solid"))
Fig2+windows(width=9, height= 5)
ggsave("C:/Users/agron/Fig2.jpg",
Fig2, width=9*2.54, height=5*2.54, units="cm", dpi=1000)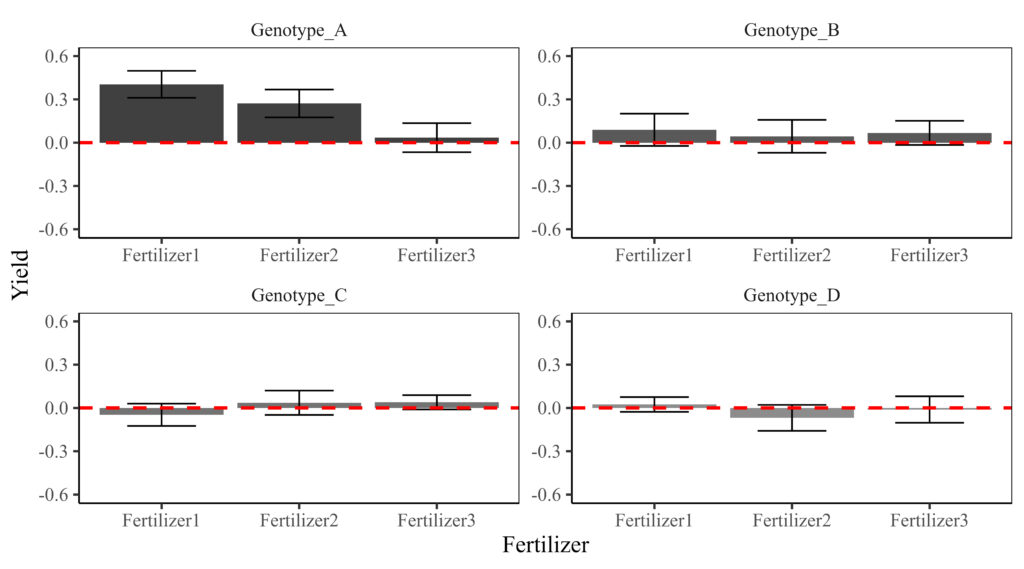
However, one of my alumni friends in the Netherlands pointed out that the bar plot is meant for nominal data or counts, and that in this case, a boxplot would be better. So, I’ll create a boxplot.
Fig3=ggplot(data=subset(df1, variable!="Control"), aes(x=variable, y=responsive_value, fill=Genotype)) +
geom_boxplot() +
scale_fill_manual(values=c("grey25","grey35","grey45","grey55"))+
scale_y_continuous(breaks = seq(-1, 1, 0.5), limits = c(-1, 1)) +
geom_hline(yintercept=0, linetype="dashed", color="red", size=1) +
facet_wrap(~ Genotype, scales="free") +
labs(x="Fertilizer", y="Yield") +
theme_classic(base_size= 15, base_family = "serif") +
theme(legend.position="none",
legend.title=element_blank(),
legend.key=element_rect(color="white", fill=alpha(0.5)),
legend.text=element_text(family="serif", face="plain",
size=13, color="black"),
legend.background= element_rect(fill=alpha(0.5)),
panel.border= element_rect(color="black", fill=NA, linewidth=0.5),
axis.line= element_line(linewidth= 0.5, colour= "black"),
strip.background=element_rect(color="white",
linewidth=0.5, linetype="solid"))
Fig3+windows(width=9, height= 5)
ggsave("C:/Users/agron/Fig3.jpg",
Fig3, width=9*2.54, height=5*2.54, units="cm", dpi=1000)
This graph illustrates how yield at different fertilizer levels responds relative to the control. Compared with the previous graph, it clearly highlights the yield differences from the control for each genotype. Genotype A appears to show greater responsiveness at Fertilizer 1 and 2, suggesting that Fertilizers 1 and 2 are beneficial for improving yield in Genotype A. In contrast, the fertilizer effect is minimal in Genotypes B, C, and D.

[Tip] descriptivestat() package
If it’s better to use just the mean and error bars to present responsiveness, I recommend using the descriptivestat() package.
# upload required package
if(!require(remotes)) install.packages("remotes")
if (!requireNamespace("descriptivestat", quietly = TRUE)) {
remotes::install_github("agronomy4future/descriptivestat", force= TRUE)
}
library(remotes)
library(descriptivestat)
# to calculate descriptive statistics
df2= descriptivestat(data= df1, group_vars= c("Genotype"),
value_vars= c("responsive_value"),
output_stats= c("se"))Fig4= ggplot() +
geom_jitter(data= subset(df2, category=="observed"),
aes(x= variable, y= responsive_value), width=0.2, alpha=0.7,
size=2, color="gray75") +
geom_errorbar(data= subset(df2, category=="mean"),
aes(x= variable, ymin= responsive_value-sd.responsive_value,
ymax=responsive_value+sd.responsive_value),
width= 0.1, color= "black") +
geom_point(data= subset(df2, category=="mean"),
aes(x= variable, y= responsive_value, fill= Genotype, shape=Genotype),
size=4, color="black") +
scale_fill_manual(name="Genotype",
values= c("orange", "red", "blue","purple")) +
scale_shape_manual(name="Genotype",
values = c(21,21,21,21)) +
scale_y_continuous(breaks=seq(-1,1,0.5), limits = c(-1,1)) +
facet_wrap(~ Genotype, scales = "free") +
labs(x= NULL, y="Responsiveness") +
theme_classic(base_size=18, base_family="serif") +
theme(
legend.position="none",
legend.key=element_rect(color="white", fill="white"),
legend.text=element_text(family="serif", face="plain",
size=15, color= "black"),
legend.background=element_rect(fill=alpha("white", 0.5)),
strip.background= element_rect(color="white", linewidth=0.5, linetype="solid"),
panel.border= element_rect(color="black", fill=NA, linewidth=0.5),
panel.grid.major= element_line(color="grey90", linetype="dashed"),
axis.line= element_blank()
)
Fig4+windows(width=9, height= 5)
ggsave("C:/Users/agron/Fig4.jpg",
Fig4, width=9*2.54, height=5*2.54, units="cm", dpi=1000)

We aim to develop open-source code for agronomy ([email protected])
© 2022 – 2025 https://agronomy4future.com – All Rights Reserved.
Last Updated: 09/06/2025