[데이터 칼럼] 선형 보간법 (Linear Interpolation) 을 사용하여 중간 데이터를 예측해 보자
오늘은 데이터 사이에 있는 값을 예측하기 위한 선형 보간법 (Linear Interpolation) 에 대해 설명하겠습니다. 예를 들어, 현장에서 데이터를 수집할 때 매일 데이터를 수집할 수는 없을 것입니다. 그래서 우리는 일정한 간격 (매주, 격주, etc.,) 으로 데이터를 수집합니다. 그러나 데이터를 제시할 때는 일별로 표시해야 할 경우가 발생 합니다. 예를 들어, 질소 비료 시비량이 0kg/ha, 30kg/ha, 60kg/ha, 120kg/ha 일 때 반응하는 작물의 수확량 차이를 조사한다고 가정해 보겠습니다. 0부터 120까지의 각 질소 비료량에서 수확량 차이를 나타내야 한다면 어떻게 데이터를 추정할 수 있을까요? 이런 상황에서 우리는 보간법 공식을 사용할 수 있습니다.
데이터를 가지고 예시를 들어 보겠습니다.
sulphur=c(0,5,10,12,15,20,24,26,30,35)
yield=c(4.1,6.2,7.5,8.2,8.8,9.5,10.5,10.4,10.1,10)
dataA=data.frame(sulphur,yield)
print(dataA)
sulphur yield
1 0 4.1
2 5 6.2
3 10 7.5
4 12 8.2
5 15 8.8
6 20 9.5
7 24 10.5
8 26 10.4
9 30 10.1
10 35 10.0황 (Sulphur) 은 작물의 성장, 영양분 흡수, 품질 향상 등 여러 측면에서 중요한 역할을 합니다. 그리고 이는 일반적으로 황산칼리 (SOP) 비료 형태로 사용됩니다. 이제 이 데이터를 바탕으로 각기 다른 SOP 양에 대한 최종 작물 수확량을 그래프를 만들어 보겠습니다.
if(!require(ggplot2)) install.packages("ggplot2")
library(ggplot2)
if (require("ggpmisc") == F) install.packages("ggpmisc")
library(ggpmisc)
ggplot(data=dataA, aes(x=sulphur, y=yield))+
stat_smooth(method='lm', linetype=1, se=FALSE,
formula=y~poly(x,2, raw=TRUE), size=0.5, color="dark red") +
geom_point(alpha=0.5, size=4) +
#Equation
stat_poly_eq(aes(label= paste(..eq.label.., sep= "~~~")),
label.x=0.9, label.y=0.9,
eq.with.lhs= "italic(hat(y))~'='~", eq.x.rhs= "~italic(x)",
coef.digits=3, formula=y~poly(x,2, raw=TRUE), parse=TRUE, size=5)+
# R-squared
stat_poly_eq(aes(label=paste(..rr.label.., sep= "~~~")),
label.x=0.9, label.y=0.85, rr.digits=3,
formula=y~poly(x,2, raw=TRUE), parse=TRUE, size=5) +
scale_x_continuous(breaks = seq(0,35,5), limits = c(0,35)) +
scale_y_continuous(breaks = seq(0,15,5), limits = c(0,15)) +
labs(y="Yield (ton/ha)", x="Sulfur application (kg/ha)") +
theme_classic(base_size=18, base_family="serif")+
theme(axis.line=element_line(linewidth=0.5, colour="black")) +
windows(width=5.5, height=5)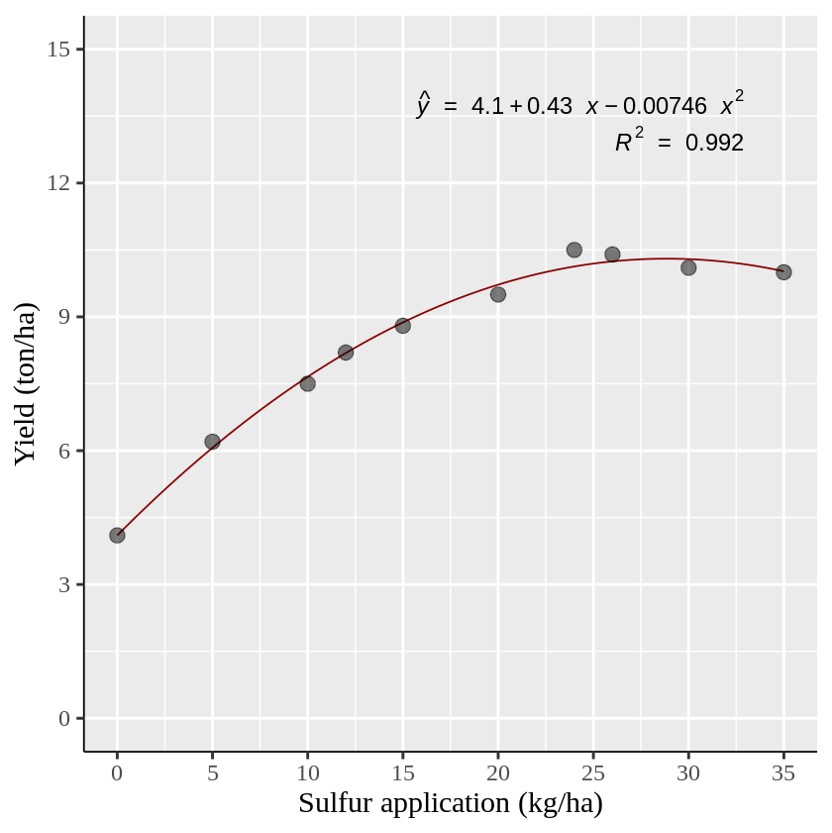
이제 위와 같은 이차 회귀 그래프를 만들었습니다. 그러나 특정 황 (Sulfur) 양에서 각 데이터 포인트를 표시해야 할 경우에는 어떻게 해야 할까요?
이를 위해 보간 (interpolation) 공식을 사용할 수 있으며, 해당 식은 다음과 같습니다:
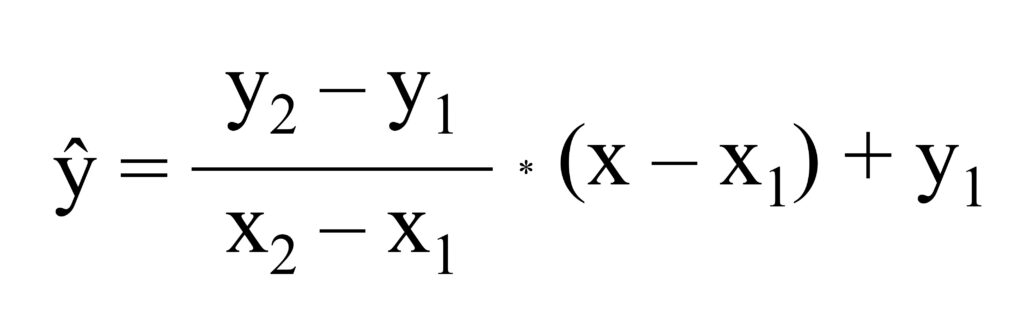
공식이 조금 까다로워 보일 수 있지만, 원리를 이해하면 식은 간단합니다. 아래 엑셀 데이터를 가지고 이야기 해 봅시다.
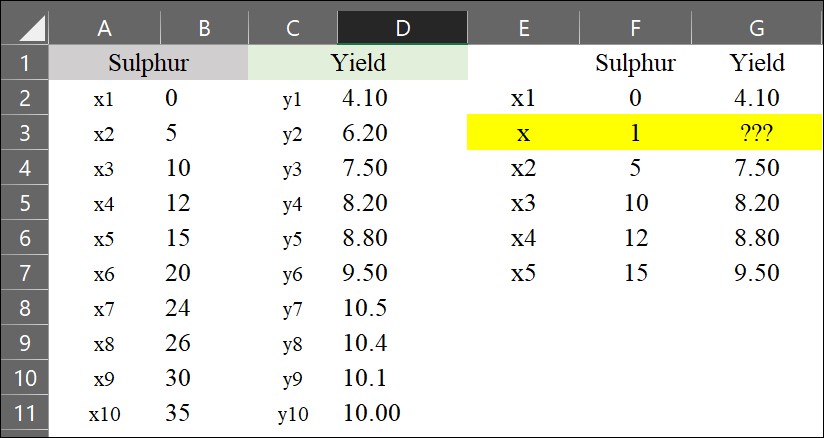
이제 황 (Sulfur) 시비량이 1 kg/ha일 때의 수확량 (yield)을 추정하고자 합니다. 이를 위해 간단한 interpolation 공식을 사용할 수 있습니다.
y= ((6.20 - 4.10) / (5 - 0)) * (1 - 0) + 4.10 = 4.52
황 (Sulfur) 시비량이 1 kg/ha일 때 수확량은 4.52 Mg/ha로 계산됩니다. 하지만 이렇게 하나하나 계산하는 것은 시간이 많이 걸리는 작업이므로, 엑셀에서 interpolation 공식을 가장 쉽게 적용하는 방법을 소개하겠습니다.
1) 기울기 계산
아래 계산식을 다시 한번 생각해 봅시다.
(y2 - y1) / (x2 - x1) = ((6.20 - 4.10) / (5 - 0)) = 0.42
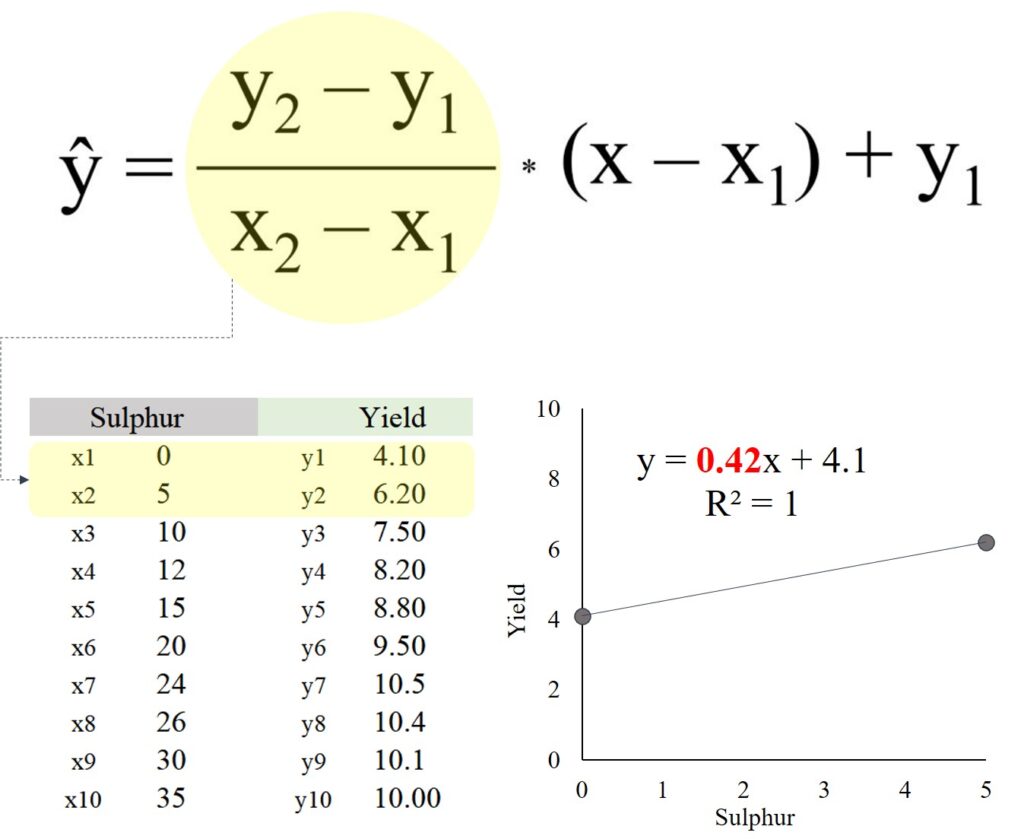
사실, 이 공식은 두 데이터 포인트 사이의 기울기(slope)를 계산하는 것입니다. 따라서 먼저 엑셀에서 각 데이터 사이의 기울기를 계산해야 합니다. 이를 위해 =SLOPE() 함수를 사용할 수 있습니다.
= slope (y range, x range)
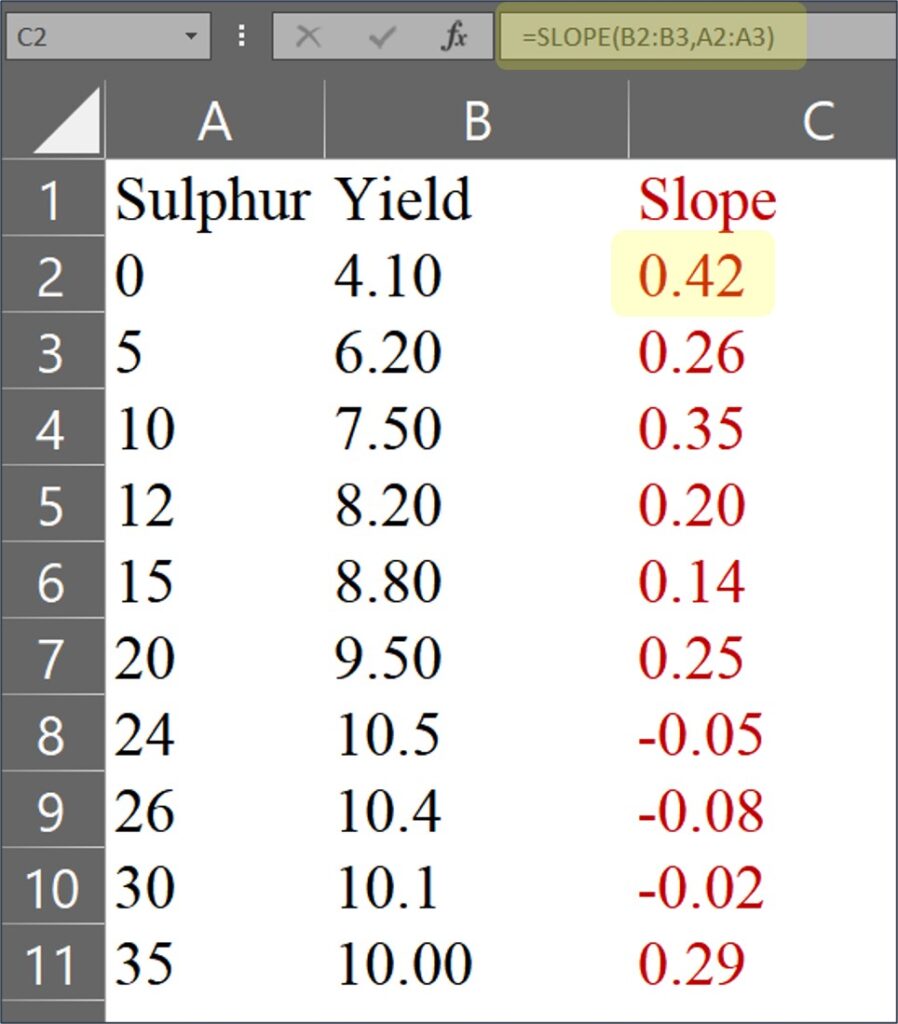
마지막 데이터인 0.29 는 10.00 / 35 ≈ 0.29 로 계산됩니다. 이유인 즉, 마지막에는 x2, y2 데이터가 존재하지 않기에 아래와 같이 계산 될 것 입니다.
(y2 - y1) / (x2 - x1) = ((100) / (35)) = 0.29
2) 가장 근접한 값 찾기
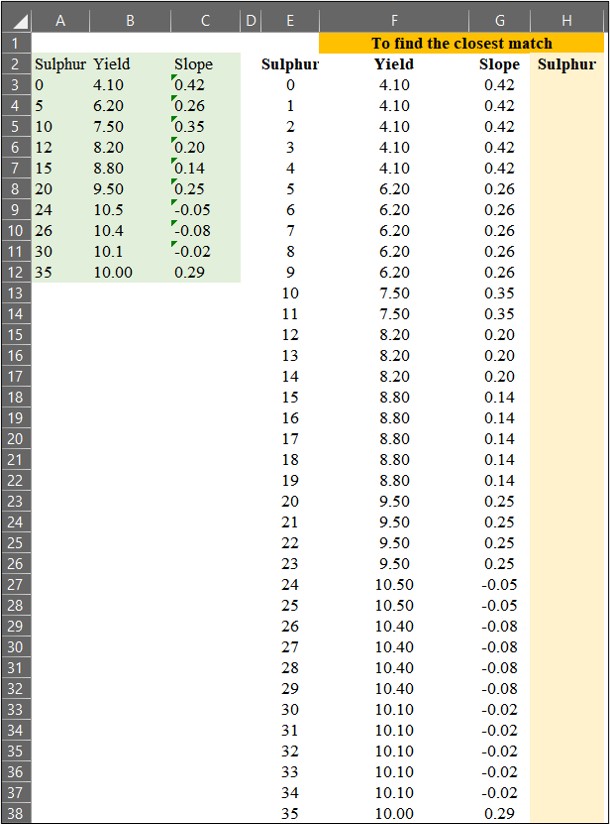
이제 황 (Sulfur) 시비량 데이터를 1에서 35까지 확장한 뒤, 원래 데이터와 비교하여 가장 가까운 값을 찾아 보겠습니다.
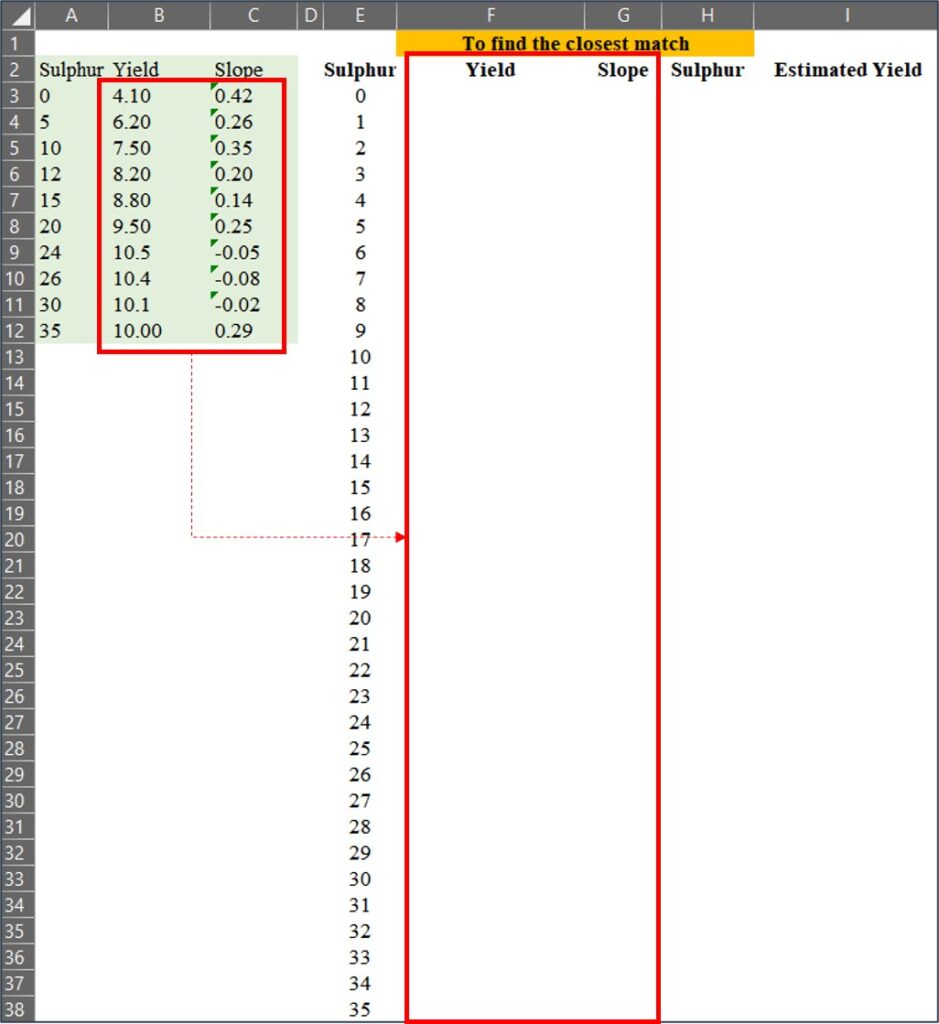
우리는 =VLOOKUP() 함수를 사용하여 데이터를 매칭할 수 있습니다. 이때, Range_lookup을 TRUE (또는 1) 로 설정하면 가장 가까운 값을 찾고, FALSE (또는 0) 로 설정하면 정확한 값을 찾습니다.
=VLOOKUP() 함수를 사용하여 확장된 황 (Sulfur) 시비량 데이터 에서 원래 데이터의 수확량 (Yield)과 기울기 (Slope) 값을 매칭해 보겠습니다.
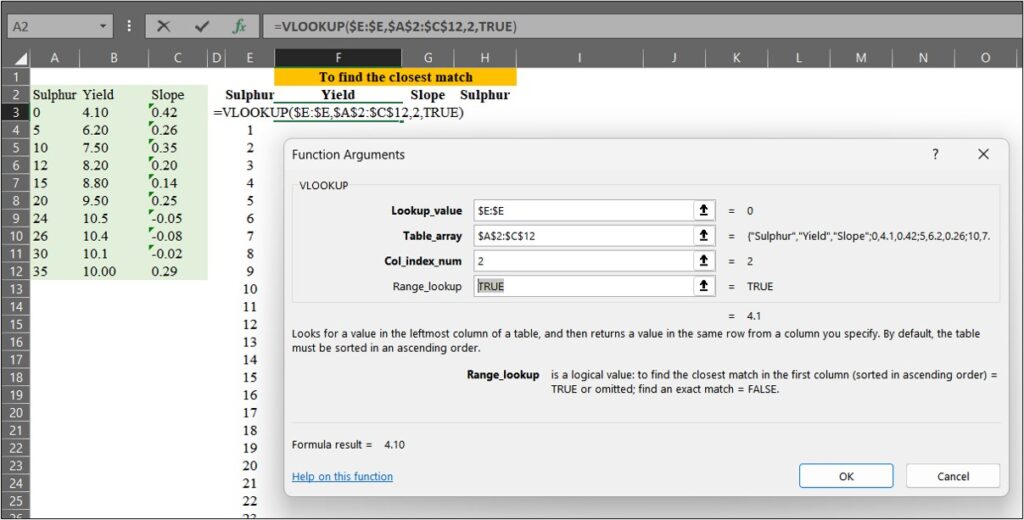
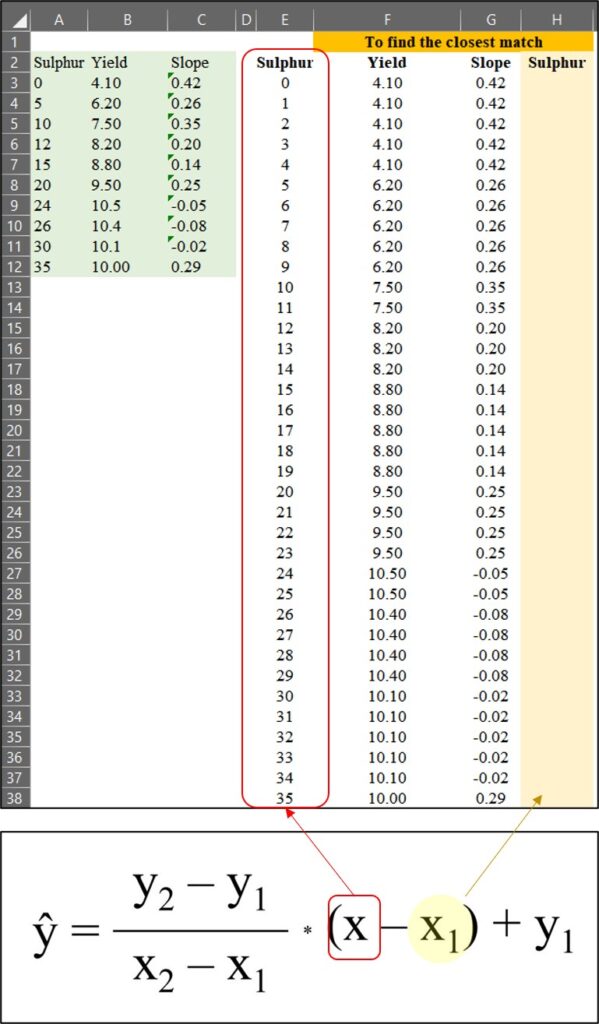
다음으로, 황 (Sulfur) 값이 있는 H 열에서 가장 가까운 값을 찾겠습니다. 이 과정은 아래의 공식과 관련이 있습니다.
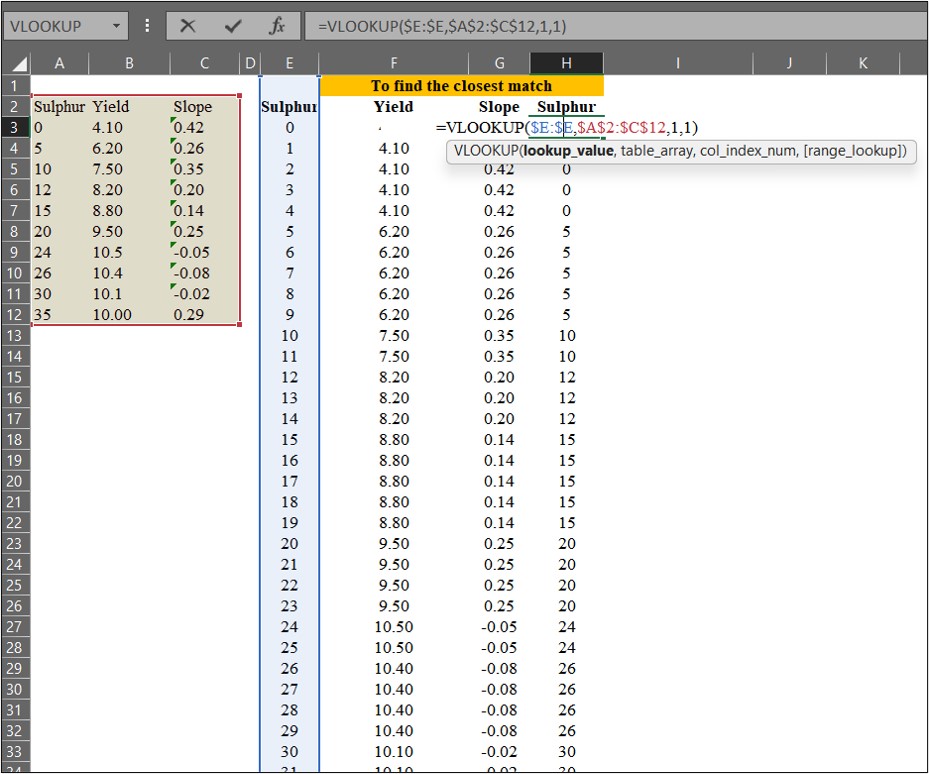
3) 예측값 계산
마지막으로, interpolation 공식을 사용하여 예측값을 계산하겠습니다.

0에서 35까지의 각 황(Sulfur) 시비량에 대한 예상 수확량을 다음과 같이 계산했습니다.
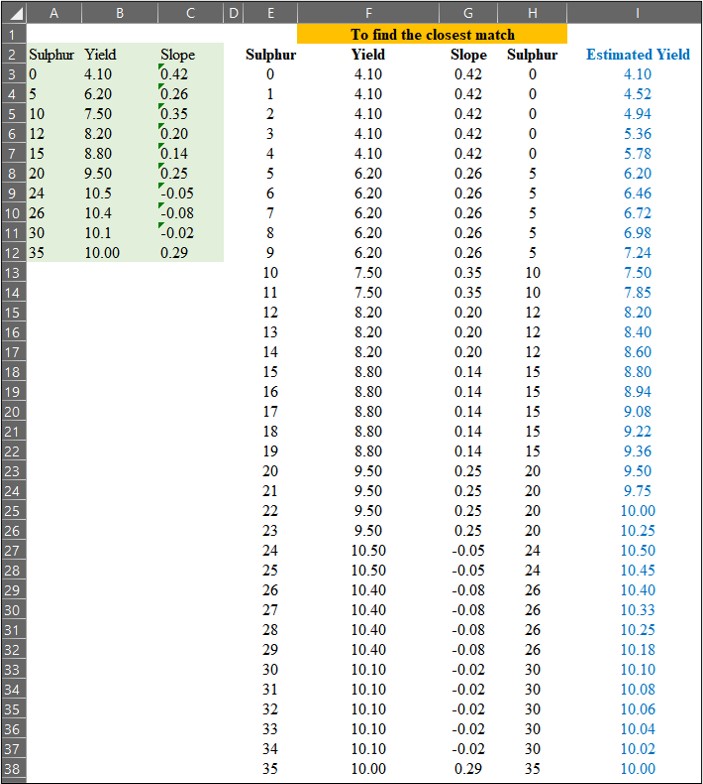
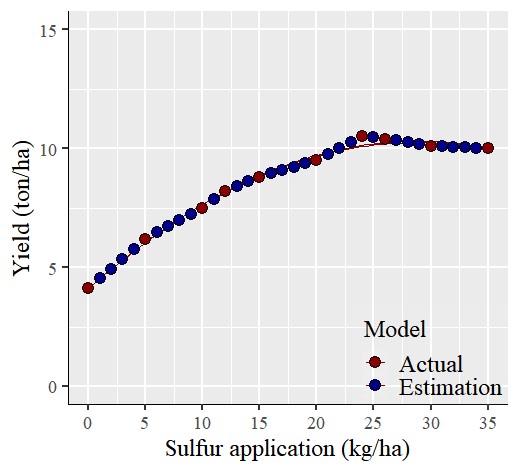
이제 각 황(Sulfur) 시비량에 대한 예상 수확량 계산을 완료했습니다. 파란색 데이터는 예측된 (보간된) 데이터를 나타내고 빨간색 데이터는 실제 측정된 데이터를 나타냅니다.
Sulphur Yield Slope Estimated.Yield
1 0 4.1 0.4200000 4.100
2 1 4.1 0.4200000 4.520
3 2 4.1 0.4200000 4.940
4 3 4.1 0.4200000 5.360
5 4 4.1 0.4200000 5.780
6 5 6.2 0.2600000 6.200
7 6 6.2 0.2600000 6.460
8 7 6.2 0.2600000 6.720
9 8 6.2 0.2600000 6.980
10 9 6.2 0.2600000 7.240
11 10 7.5 0.3500000 7.500
12 11 7.5 0.3500000 7.850
13 12 8.2 0.2000000 8.200
14 13 8.2 0.2000000 8.400
15 14 8.2 0.2000000 8.600
16 15 8.8 0.1400000 8.800
17 16 8.8 0.1400000 8.940
18 17 8.8 0.1400000 9.080
19 18 8.8 0.1400000 9.220
20 19 8.8 0.1400000 9.360
21 20 9.5 0.2500000 9.500
22 21 9.5 0.2500000 9.750
23 22 9.5 0.2500000 10.000
24 23 9.5 0.2500000 10.250
25 24 10.5 -0.0500000 10.500
26 25 10.5 -0.0500000 10.450
27 26 10.4 -0.0750000 10.400
28 27 10.4 -0.0750000 10.325
29 28 10.4 -0.0750000 10.250
30 29 10.4 -0.0750000 10.175
31 30 10.1 -0.0200000 10.100
32 31 10.1 -0.0200000 10.080
33 32 10.1 -0.0200000 10.060
34 33 10.1 -0.0200000 10.040
35 34 10.1 -0.0200000 10.020
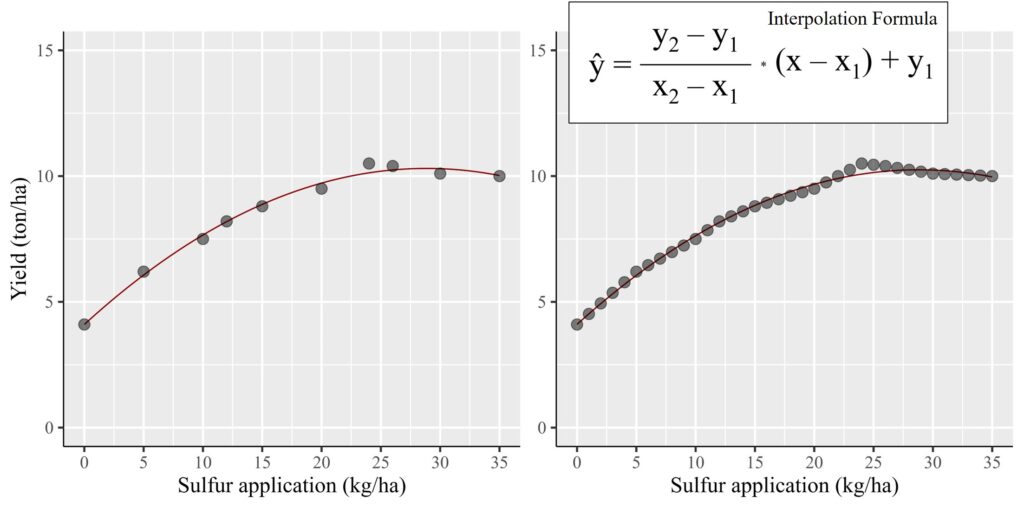
36 35 10.0 0.2857143 10.000비교를 시각적으로 확인하기 위해 두개의 그래프를 그려 보겠습니다. 왼쪽 그래프는 실제 데이터를 가지고 그래프를 그렸고, 오른쪽 그래프는 보간된 (예측된) 데이터를 가지고 그래프를 그렸습니다. 통계적 결과 (기울기 및 R²) 가 크게 변하지 않는 것을 확인 할 수 있는데 이는 보간된 데이터가 실제 데이터의 범위 내에 존재하기 때문입니다.
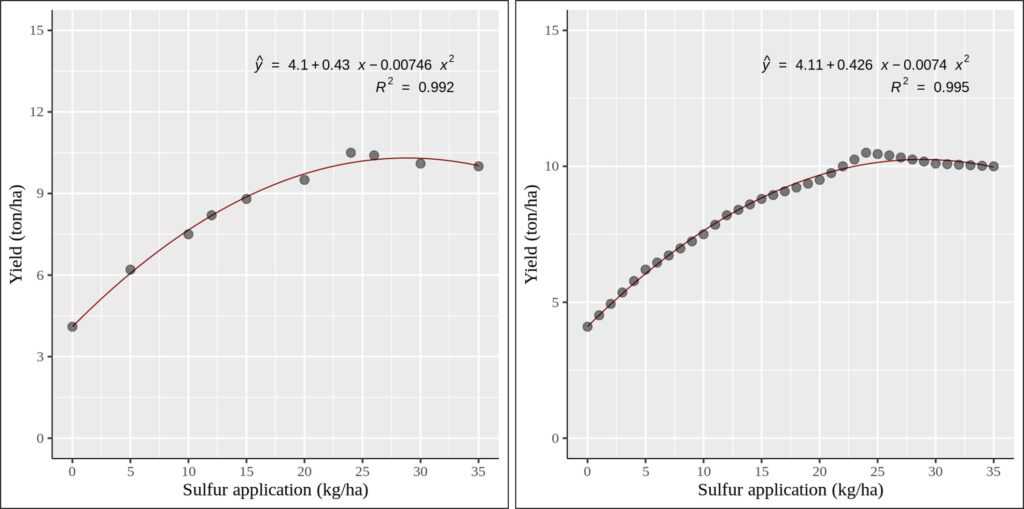
이것이 보간 (interpolation) 기법을 사용하여 중간 데이터를 예측하는 방법입니다.독립 변수의 전체 범위에 대해 종속 변수를 표현해야 하는 경우, 이 보간 기법을 활용하여 신뢰할 수 있는 값을 추정할 수 있습니다.
■ R 을 이용하여 중간 데이터 값을 예측
이제 보간법의 원리를 이해했다면, 앞에서 처럼 단계별로 계산할 필요 없이 R을 이용하여 간편하게 계산할 수 있습니다. 아래 코드를 참조해 주세요.
sulphur= c(0,5,10,12,15,20,24,26,30,35)
yield= c(4.1,6.2,7.5,8.2,8.8,9.5,10.5,10.4,10.1,10)
dataA= data.frame(sulphur, yield)# Install and load the zoo package
if(!require(zoo)) install.packages("zoo")
library(zoo)
# Create a sequence for the complete range of sulphur
full_range= seq(min(dataA$sulphur), max(dataA$sulphur))
# Interpolate the values for yield
yield_interp= na.approx(dataA$yield, x= dataA$sulphur, xout= full_range)
# Combine the results into a new data frame
df_interp= data.frame (sulphur= full_range, yield= yield_interp)
head (df_interp, 3)
sulphur yield
0 4.10
1 4.52
2 4.94
.
.
.
tail (df_interp, 3)
sulphur yield
33 10.04
34 10.02
35 10.00if(!require(ggplot2)) install.packages("ggplot2")
library(ggplot2)
if(!require(ggpmisc)) install.packages("ggpmisc")
library(ggpmisc)
ggplot(data=df_interp, aes(x=sulphur, y=yield))+
stat_smooth(method='lm', linetype=1, se=FALSE,
formula=y~poly(x,2, raw=TRUE), size=0.5, color="dark red") +
geom_point(alpha=0.5, size=4) +
#Equation
stat_poly_eq(aes(label= paste(..eq.label.., sep= "~~~")),
label.x=0.9, label.y=0.9,
eq.with.lhs= "italic(hat(y))~'='~", eq.x.rhs= "~italic(x)",
coef.digits=3, formula=y~poly(x,2, raw=TRUE), parse=TRUE, size=5)+
# R-squared
stat_poly_eq(aes(label=paste(..rr.label.., sep= "~~~")),
label.x=0.9, label.y=0.85, rr.digits=3,
formula=y~poly(x,2, raw=TRUE), parse=TRUE, size=5) +
scale_x_continuous(breaks = seq(0,35,5), limits = c(0,35)) +
scale_y_continuous(breaks = seq(0,15,5), limits = c(0,15)) +
labs(y="Yield (ton/ha)", x="Sulfur application (kg/ha)") +
theme_classic(base_size=18, base_family="serif")+
theme_grey(base_size=18, base_family="serif")+
theme(axis.line=element_line(linewidth=0.5, colour="black"))+
windows(width=5.5, height=5)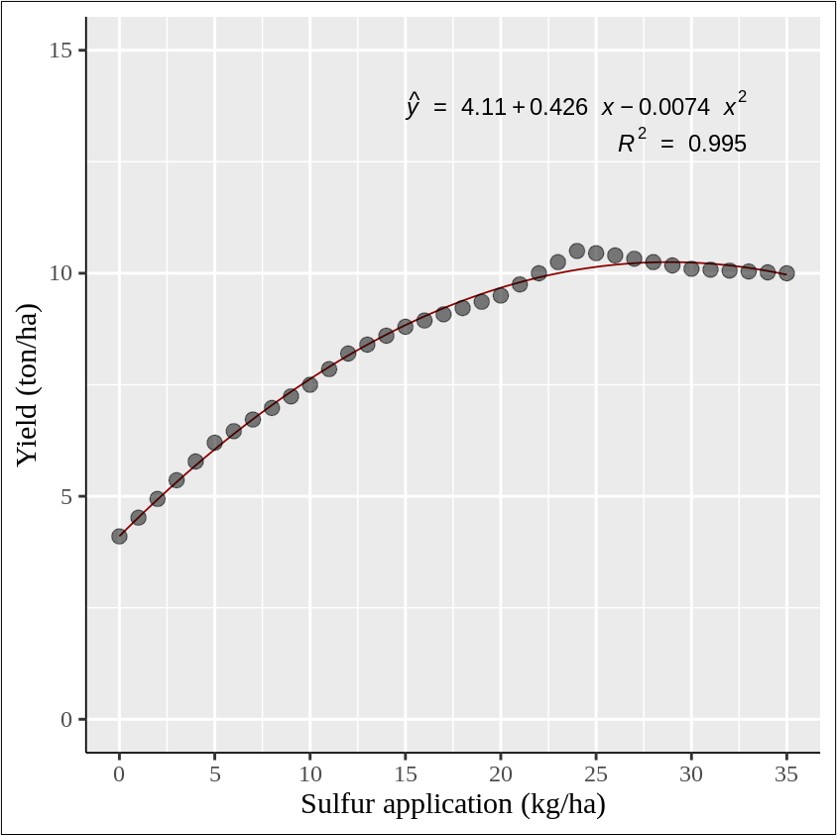
Full code: https://github.com/agronomy4future/r_code/blob/main/Predicting_Intermediate_Data_Points_with_Linear_Interpolation_in_Excel_and_R.ipynb
■ R 패키지: interpolate()
얼마전 저는 중간 데이터 값을 쉽게 계산하기 위해 새로운 R package; interpolate() 를 개발 했습니다.
sulphur= c(0,5,10,12,15,20,24,26,30,35)
yield= c(4.1,6.2,7.5,8.2,8.8,9.5,10.5,10.4,10.1,10)
dataA= data.frame(sulphur, yield)
if(!require(remotes)) install.packages("remotes")
if (!requireNamespace("interpolate", quietly = TRUE)) {
remotes::install_github("agronomy4future/interpolate", force= TRUE)
}
library(remotes)
library(interpolate)
result= interpolate(dataA, x="sulphur", y="yield", group_vars= NULL)
print (result)
sulphur yield category
1 0 4.100 0
2 1 4.520 1
3 2 4.940 1
4 3 5.360 1
5 4 5.780 1
6 5 6.200 0
7 6 6.460 1
8 7 6.720 1
9 8 6.980 1
10 9 7.240 1
11 10 7.500 0
12 11 7.850 1
13 12 8.200 0
14 13 8.400 1
15 14 8.600 1
16 15 8.800 0
17 16 8.940 1
18 17 9.080 1
19 18 9.220 1
20 19 9.360 1
21 20 9.500 0
22 21 9.750 1
23 22 10.000 1
24 23 10.250 1
25 24 10.500 0
26 25 10.450 1
27 26 10.400 0
28 27 10.325 1
29 28 10.250 1
30 29 10.175 1
31 30 10.100 0
32 31 10.080 1
33 32 10.060 1
34 33 10.040 1
35 34 10.020 1
36 35 10.000 0
이 코드는 자동으로 interpolation 을 계산할 뿐만 아니라, 각 데이터가 실제 데이터 (0) 인지 보간된 데이터(1) 인지 구분하여 표시합니다. 자세한 내용은 아래 게시물을 참고해 주세요.
■ [R package] An easy way to use interpolation code to predict in-between data points

We aim to develop open-source code for agronomy ([email protected])
© 2022 – 2025 https://agronomy4future.com – All Rights Reserved.
Last Updated: 01/03/2025
Your donation will help us create high-quality content.
PayPal @agronomy4furure / Venmo @agronomy4furure / Zelle @agronomy4furure